|

Photo: from a DECsystem-10 sales brochure, courtesy of Michael Thompson, Retro-Computing Society of RI.
To put this 1971 article in context, most Technical Colleges were only just getting equipped with a computer in 1971 and the computer would be driven by punch cards or tape and output was to a line printer. In some cases Teletype terminals allowed on-line sessions. The VDU was only just being developed and the first 4 bit microprocessor, the Intel 4004 housed in a 16 pin DIL chip, was released that year. Most computers used magnetic tape for storage.
In 1971 I watched a mainframe being assembled in a data centre and the brand new feature was a hard disk. This came in sections on pallets and was built on site. The single platter was about 800 mm in diameter and 8 mm thick. It had 24 static heads and the platter was spun by a large AC motor of several HP. The capacity of this monster was 8 Mb. The picture below of the PDP10 shows the large 'washing machine' multi platter disk drives. The packs were removable and the heads were positioned by a large voice coil motor about 120 mm diameter and 200 mm long.
The article is in the original basic but the re-worked source code and GW-BASIC interpreter can be downloaded by right clicking and saving-as. The same method will copy the data file to your disk.
Introduction
As a member of the VHF Contests Committee, the author was intrigued to receive a 2m contest entry, in which the distance calculations had been made by a computer, and in an accompanying letter the entrant offered to make the program available to anyone who was interested. At the time the author had no access to a computer, but later access to a time-sharing computer terminal became available. After an introductory course to computer programming and a number of weeks' use of the computer, the author again considered the possibility of using the contestant's program, and from him he received the complete program plus a full set of punched cards.
There were, unfortunately, two snags. The first was that the computer terminal used was a tape reader (ie the information was fed into it on punched paper tape) and so the cards could not be used. The second was that all the author's programming had been done in the language BASIC, while this program used FORTRAN. This did not appear to be insurmountable as the time-sharing computer has a FORTRAN compiler also, but it was discovered that there are many different versions of FORTRAN and these two versions were not the same. Without the necessary knowledge to convert the program, it was decided to start from scratch and write a program as an exercise in BASIC programming. The aim was to write a program that required for information only the QRA locators encountered in the contest to produce:
- The distance worked to each station (km);
- the score on the RSGB radial scoring system;
- the total score, and
- the longest distance contact.
The program was duly written and after a lot of 'de-bugging' was induced to work. This it did very well, fulfilling all the stated objectives. As an exercise in computer programming and logical thinking it was invaluable. While it is written in BASIC, which is a language commonly used with time-sharing computers, the program can, of course, be re-written in different languages, and the following explanation will assist in the understanding of the logical steps involved.
It does not attempt to give a full explanation of the derivation of the QRA locator system. For a fuller understanding of this see [1] and [2]. Similarly, for a fuller explanation of the BASIC language see [3].
The Program
The full text of the program is here. Its basis is the determination of the latitude and longitude of the base station and the stations contacted, using their QRA locators.
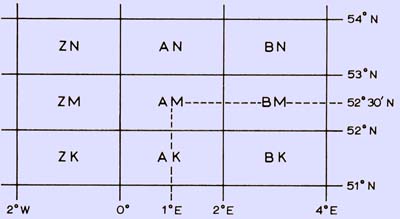
Primary squares of the QRA locator system.
This is done 'manually' as follows, using the author's own locator AM61G as an example: The co-ordinates of the centre of the secondary square (below) are determined relative to the centre of the primary square (above), and the increments of latitude and longitude are added or subtracted as appropriate.
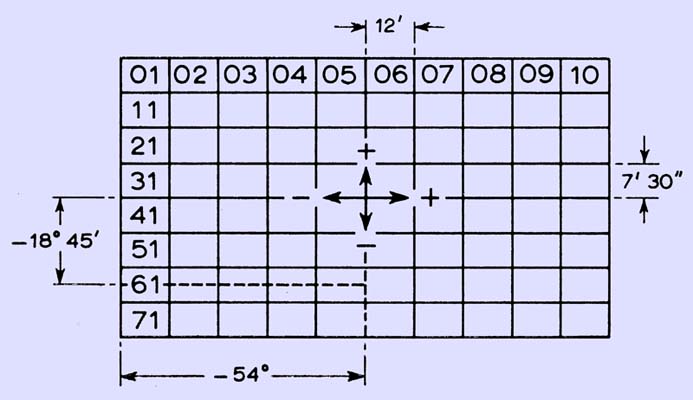
Secondary squares (Note the original image says ° it should read ')
Finally, the centre of the tertiary square is found by further increments to the previously determined co-ordinates (below).
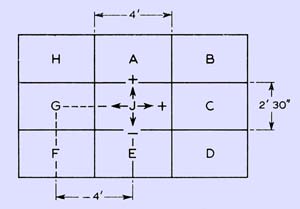
Tertiary squares.
n our example, the 'X' co-ordinate is latitude and the 'Y' co-ordinate is, longitude. The location to convert to QRA is 2'E and 52°11'15''N. The primary square covering this map reference is AM with its centre at 1°E and 52°30'N. Next the secondary square is found, in our case we need -54'E and -18'45''N and this is square 61. The last letter is the tertiary square and we need -4'E and this is G. For ease of calculation, minutes and seconds are taken as decimal parts of a degree.
In the detailed program explanation, east and north are positive, and west and south are negative for calculation purposes. The numbers which precede each computer statement are 'line numbers' and serve as identification. The program starts at line 100:
100 FILES QRA
The main program contains the instructions to the computer on how to process the information it is given. This information is contained in a separate part of the computer store called a 'data file' which is called up by the 'statement 'FILES QRA'.
This data file contains:
- The contest title;
- the entrant's callsign;
- the entrant's QRA locator which is the reference point for all the
- distance calculations, and
- the QRA locator of all the stations contacted in the contest.
In addition to this information the file may contain the letters 'NS'. This is to cater for the situation where a serial number and report are sent but for various reasons neither are received and the contact is not completed. This allows the serial numbers in the computer print-out to correspond with the serial numbers in the contest log. The last piece of information in the data file must be the word 'END' which instructs the computer to print the total score and the longest distance contact.
The '$' suffix indicates that the group to which the symbol is designated contains an alphanumeric string. To perform calculations the computer must use numbers.
110 DIM N$(26)
120 FOR I = 1 TO 26
130 READ N$(I)
140 NEXT I
150 DATA U,V,W,X,Y,Z,A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T
However, the QRA locator contains letters as well as numbers and these must be coded with numbers to allow these numerical calculations to be performed. Line 110 reserves sufficient space in the computer store to accommodate the table which is about to be entered. Line 120 initially takes the value of 1 for I. Line 130 makes N$(I) equal to the first letter in the DATA line 150 which is 'U'. Line 140 switches the program back to line 120 and takes the next value of I which is 2. Thus N$(2) = V, N$(3) = W, N$(4) = X. ... N$(24) = R, N$(25) = S, N$(26) = T.
The reason for the first letter being 'U' and not 'A' will be apparent later. This code enables simple equations to be derived to calculate the co-ordinates of the primary square from the first two letters of the QRA locator.
160 FOR I=1 TO 9170 READ Q$(I),P(I),Q(I)
180 NEXT I
190 DATA A,0,0.0417,B,0.0667,0.0417,C,0.0667,0,D,0.0667,-0.0417,
200 DATA E,0,-0.0417,F,-0.0667,-0.0417,G,-0.0667,0,H,-0.0667,
210 DATA 0.0417,J,0,0
Unfortunately it is not easy to derive equations to determine mathematically the increments to latitude and longitude designated by the last letter of the QRA locator. Thus for simplicity the actual values are entered into the computer as a table. For example, 'G': Increment to X = -0.06670, increment to Y = 00. That is. Q$(7) = G, P(7) = -0-0667, Q(7) = 0.
220 READ #1,A$,B,C$,D$
This line reads from the data file:
A$ - The month of the contest;
B$ - the frequency band;
C$ - the type of contest (eg open, portable etc);
D$ - the entrant's callsign.
230 GOSUB 700
This line routes the program to a subroutine which takes the QRA locator and calculates its latitude and longitude as x and y co-ordinates. At the end of the subroutine the program is routed back to the line after the GOSUB statement.
240 LET X0=X*0.0175
250 LET Y0=Y*0.0175
The co-ordinates which have been derived in degrees in the subroutine are converted into radians since the computer can only work in radial co-ordinates.
260 PRINT
270 PRINT A$;" 1970";B;"MHZ ";C$;" CONTEST"
280 PRINT "CONTEST ENTRY OF ";D$;" LOCATED AT ";M$;K$;C;F;R$
On a line containing only the command PRINT as in 260, the computer steps a line without printing anything. In lines 270 and 280 the titles are printed, containing the information specific to the contest. M$, K$, C, F and R$ are the alphanumerics of the QRA locator and are read from the data file in the subroutine.
290 PRINT
300 PRINT "SERIAL NO. ","QRA","DISTANCE (KMS) ","POINTS"
310 PRINT "----------------------------------------------------"
Line 300 prints the headings and line 310 improves the presentation by underlining the headings.
320 LET K=K+l
K is the serial number. This line increases the previous serial number by 1 to provide the serial number sequence.
330 GOSUB 700
This performs the same function as line 230.
340 LET Xl=X*0.0175
350 LET Yl=Y*0.0175
As in lines 240 and 250, the co-ordinates of the station contacted are converted into radial co-ordinates.
360 LET U1=ABS(X1-X0)
370 LET U2=(COS(Y0)*COS(Y1)*COS(U1))+(SIN(Y0)*SIN(Y1))
380 LET U3=ATN(SQR((1-(U2)^2)/(U2)^2))
390 LET Z=INT((6371*U3)+0.5)
The initial calculation to find the distance to the station contacted is to find the angle subtended at the centre of the earth (which is assumed to be a sphere) by the two stations (θ). The equation to determine this is in line 370. The * indicates multiplication to the computer and ^ indicates an exponent.
θ = cos¯¹[(cos(Y0) × cos(Y1) × cos(X1 - X0)) + (sin(Y0) × sin(Y1))] . . . [1]
Where:
Y0 = Y co-ordinates of the base station
Y1 = Y co-ordinates of the other station
X0 = X co-ordinates of the base station
X1 = X co-ordinates of the other station.
The equation used in the program is altered so that θ can be determined by taking tan¯1(f), since the computer used by the author only calculates Arctan,
The length of the arc between the two stations = Rθ where R = radius of the earth,
For the earth, R = 6,371km (average) or 3,959 miles.
Therefore, Distance (Z) = 6,371 X θ km or 3,959 X θ miles.
The value of Z is rounded to the nearest kilometre since the locator system itself and the approximation of R do not warrant greater accuracy.
400 IF Z GE 200 THEN 440
410 IF Z GE 1000 THEN 460
420 LET S=50
430 GOTO 470
440 LET S=(INT(Z/50.1)*2)+1
450 GOTO 470
460 LET S=(INT(Z/100.1)*4)+2
These lines calculate the score on the R8GB radial scoring system. There are three conditions, each requiring a different equation to calculate the score (S):
- Z less than 200km. The score advances by 2 at 50km intervals
starting at 1 (0-50km). This is expressed in the equation on line 440;
- Z greater than 200km and less than l,000km. The score advances
by 4 at 100km intervals starting at 10 (200-300km). This is expressed in the equation on line 460. To ensure that Rule 5(a) of the 1970 VHF/UHF Contest Rules is complied with, the radial rings for the purposes of scoring are at multiples of 50.1km up to 200km, and multiples of 100.1km from 200 to 1,000km. Thus : contacts on borders will score low;
- above 1,000km the score is 50.
- the entrant's callsign.
470 PRINT K,M$;K$;C;R$,Z,S
The information for the specific QRA locator is now complete and the information is printed under the appropriate headings:
K = the serial number;
M$, K$, C, F, R$ = the QRA locator;
Z = the distance;
S = the score.
480 LET Sl=Sl+S
This equation compiles the score. Although the equation appears to be mathematically wrong, its meaning is: the new value of S1 is the sum of the calculated score and the previous value of S1. In this way the score is compiled. The function of the equation is explained in the following example: The first three scores in a contest are 3, 14 and 5: after the first contact, S1 = 0 + 3 = 3 ; after the second contact, S1 = 3 + 14 = 17; after the third contact, S1 = 17 + 5 = 22.
The total score is printed at the end of the results table.
These lines pick out the longest distance contact and store the distance and serial number for printing out at the end of the results table.
490 IF Z GE Z1 THEN 520
500 LET Z1=Z
510 LET K1=K
520 GOTO 320
Line 490 tests whether the value of Z is less than or equal to the previous longest distance. If it is, the program jumps to line 520 and the value of Z1 is not changed. If Z is greater than Z1 the program proceeds to line 500. Here Z1 is assigned the value of Z. Also K1 is assigned the value of K, the serial number, so that the longest distance contact can be identified. This completes all the processing necessary on the QRA locator and line 520 returns the program to line 320 where the sequence starts again with the next QRA locator.
530 PRINT K,"NON-SCORING CONTACT"
540 GOTO 320
As was explained earlier, 'NS' is entered in the data file when a contact cannot be counted for scoring purposes. In the subroutine, as will be seen, there is a line which looks for 'NS'. When it finds it, the program jumps to line 530 and prints the serial number and the words 'Non-scoring contact' in place of the normal format contained in line 470. Having done this, line 540 instructs the program to jump to line 320 where the sequence starts again with the next QRA locator.
550 PRINT
560 PRINT
510 PRINT "TOTAL SCORE =";S1
580 PRINT
590 PRINT "THE LONGEST DISTANCE CONTACT IS NO.";K1;"AT ";Z1;"KMS"
In the subroutine there is a line looking for the word 'END' in the data file. When it encounters this the program jumps to line 550 above. Lines 550 and 560 leave two blank lines, 570 prints the total score, 580 leaves a blank line, and 590 prints the longest distance contact.
600 STOP
This is self-explanatory and signifies the end of the program.
The subroutine occurs at the end of the program since it is used many times during the course of the program's execution.
700 READ #1,MS
710 IF M$="NS" THEN 530
720 IF M$="END" THEN 550
Line 700 calls up the first letter of the QRA locator from the data file and assigns it the symbol 'M$'. Line 710 checks to see if this letter is the group 'NS'. If it is, the program jumps to line 520 and proceeds as indicated previously. If 'M$' is not 'NS' then the program proceeds to line 720 where it is checked whether it is the group 'END'. If it is, the program jumps to line 540 and the program is completed as shown previously.
730 READ #1,K$,C,F,R$
If M$ is neither 'NS' or 'END' the program continues to line 730 where the remaining symbols of the QRA locator are read from the file and are assigned the symbols:
K$ = Second letter of the locator:
C = First number of the locator:
F = Second number of the locator:
R$ = Last letter of the locator:
740 FOR J=1 TO 26
750 IF M$ NE N$(J) THEN 770
760 LET X=(2*J)+(0.2*F)-14.1
The computer now refers back to the table compiled in lines 110-150. It scans the table from N$(1) to N$(26) looking for the letter that is the same as M$. When M$ does not equal N$(J) the program jumps to line 770 where it is checked to see if N$(J) is the same as the second letter of the QRA locator. When the same letter in the table as M$ is found, the value of J is used in the equation in line 760.
The equation is derived as follows:
Inspection of a QRA locator map will show that the most westerly locator likely to be encountered (on the west coast of Eire) will contain the first letter 'U'. This letter denotes a segment covering 100 West to 120 West. The centre of this segment is 110 West. The next segment to the east has the letter 'Y' and its centre is 90 West. The segments continue to the east at 20 intervals in alphabetical order. When 'Z' is reached, the next segment is 'A' (see primary squares diagram). Thus a simple equation can be derived, since in the table, in lines 110-150, the letters were coded U = 1, Y = 2, etc,
Therefore A = [2J - 13]° . . . [2]
where A = Longitude of the centre of the primary square,and J = Position of the first letter of the QRA locator in the table. The second number of the QRA locator also relates to the longitude. From the secondary squares diagram, it can be seen that numbers 1 to 5 are west of centre and numbers 6 to 0 are east of centre of the primary square. Each square is 12' (0.20) wide. Thus the difference in longitude between the centre of the primary square and the centre of the secondary square is:
L=[(0.2.F) - 1.1]° . . . [3]
This equation is not correct when F = 0 as will be shown later.
Combining the two equations above give the longitude of the centre of the secondary square (X).
X = (2.J) + (0.2.F) - 14.1 . . . [4]
This is the equation in line 760.
770 IF K$NEN$(J) THEN 790
780 LET Y=J+33.9375-(0.125*C)
790 NEXT J
While the table is being scanned, each letter in turn is also, compared with the second letter of the QRA locator (K$). If K$ is the same as N$(J), the program jumps to line 790 and the next value of J. If K$ is the same as N$(J), the value of J is used in the equation in line 780. The equation is derived as follows:
The primary squares advance in latitude steps of 10, as can be seen in the diagram above. By inspection, the equation for the latitude of the primary square (B) is
B = (1 + 33.5)° . . . [5]
where J = The position of the second letter of the QRA locator in the table.
The first number also relates to the latitude. From the secondary squares diagram it can be seen that, apart from the column to the far right, numbers 0 to 3 are north of the centre of the primary square, and numbers 4 to 7 are south.
The width of each segment is 7° 30'' = 0.1250.
Thus the difference in latitude between the centre of the primary square and the centre of the secondary square (M) is
M = (0.4375 - 0.125.C)° . . . [6]
where C = The first number of the locator.
As with equation (2), the equation is not correct when F=0.
Equations (4) and (5) can be combined to give the equation
Y = (J + 33.9375 - 0.125.C)° . . . [7]
This is the equation in line 780. Thus the latitude of the centre of the secondary square is derived. Taking again the example AM61G;
Y = 19 + 33.9375 - (0.125 x 6) = 52.18750 or 52011' 15'' North
800 IF F NE 0 THEN 830
810 LET Y=Y+0.125
820 LET X=X+2
It can be seen from the secondary squares diagram that when the second number of the QRA locator (F) is zero, the first number is not the same as the other squares at the same latitude. It is, in fact, always 1 greater. For instance, square 20 is at the same latitude as square 19 However, equation (7) would calculate that square 20 was at the same latitude as squares 21-29 whereas it is in fact 7' 30'' further north. When F = 0, the condition in line 800 is not fulfilled and the program proceeds to line 810. On this line, 7' 30'' (0.1251 is added to the latitude, thus correcting the error.
Equation (3) calculates that a secondary square with zero for its second number is west of a square with 1 for its second number, whereas it comes after 9 and is, for calculation purposes, 10. Thus equations (3) and (4) will calculate the longitude to be 10 squares (ie 2°) west of where it actually is. Thus when F = 0, line 820 adds 20 to the longitude and corrects the error.
830 FOR J=l TO 9
840 IF R$=Q$(J) THEN 860
850 NEXT J
860 LET X=X+P(J)
870 LET y=y+Q(J)
The final increments to the latitude and longitude are determined by the last letter of the QRA locator (R$). The computer scans the second table (lines 160 - 210) until the letter in the table is the same as the last letter of the QRA locator being processed. The increments to X and Y are taken from the table and added to X and Y in lines 860 and 870 respectively. In the example AM61G, the final co-ordinates are:
x = (0.1 - 0.667)° = 0.03330 or 2' East
Y = (52.1875 + 0)° = 52.18750 or 52011'15'' North
880 RETURN
999 END
The 'RETURN' command is used to determine the subroutine and literally return the program to the line immediately after the 'GOSUB' statement that initiated the use of the subroutine.
The 'END' statement is not really necessary but is good BASIC grammar.
Example
To show how the program works in practice, a contest log for an imaginary contest which the author has entered is given below.
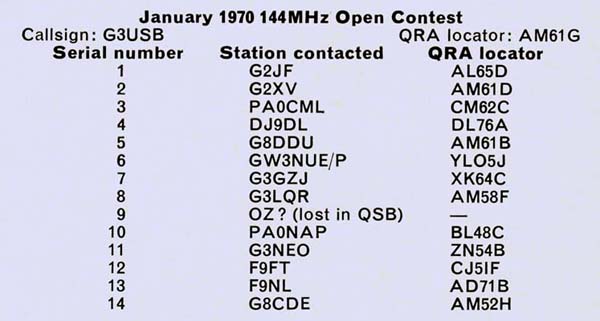
The data file is prepared on punched paper tape in the following order:
- The contest title;
- Callsign of the entrant;
- QRA locator of the entrant;
- QRA locators of all stations contacted.
- The file must be finished with the word 'END'.

This information is fed into the computer memory in the form shown in above using the data file name 'QRA'. Having done this it is saved ready for use with the main program. The main program, which is also on punched paper tape, is then fed in. On the command 'RUN' the program execution takes place, producing the result shown below.
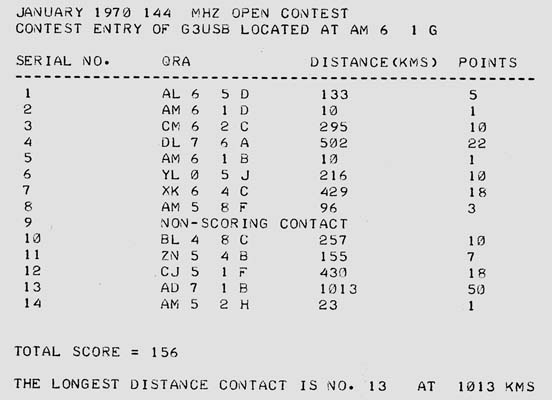
The actual time taken to do the various operations was:
- To prepare the data punched tape - 4 min;
- To feed the data tape into the computer - 20s;
- To feed the main program tape into the computer approximately 3 min 30 s;
- Time to print out the results - 2 min 15 s.
The total time is thus approximately 10 min 5 sec. Of these times (c) is constant but (a), (b) and (d) vary according to the number of stations worked in a contest.
Conclusion
The author hopes that this article is of direct value to the reader, but if it is not he hopes that it gives an insight into the logical processes involved in writing a computer program and how the use of a computer can take a lot of the tedious work and potential inaccuracy out of scoring a VHF/UHF contest.
References
- R C Hills - 'QRA locatormanship', RSGB Bulletin, March 1965, p162.
- A J Gould - 'Using the QRA locator', Radio Communication, March 1969, p173.
- GEIS Ltd - 'An introduction to programming in BASIC'.
|